Welcome to SPOTPY

A Statistical Parameter Optimization Tool for Python

Purpose

SPOTPY is a Python framework that enables the use of Computational optimization techniques for calibration, uncertainty and sensitivity analysis techniques of almost every (environmental-) model. The package is puplished in the open source journal PLoS One:

Houska, T., Kraft, P., Chamorro-Chavez, A. and Breuer, L.: SPOTting Model Parameters Using a Ready-Made Python Package, PLoS ONE, 10(12), e0145180, doi:10.1371/journal.pone.0145180, 2015

The simplicity and flexibility enables the use and test of different algorithms without the need of complex codes:

sampler = spotpy.algorithms.sceua(model_setup())     # Initialize your model with a setup file
sampler.sample(10000)                                # Run the model
results = sampler.getdata()                          # Load the results
spotpy.analyser.plot_parametertrace(results)         # Show the results

Features

Complex algorithms bring complex tasks to link them with a model. We want to make this task as easy as possible. Some features you can use with the SPOTPY package are:

• Fitting models to evaluation data with different algorithms. Available algorithms are Monte Carlo (MC), Markov-Chain Monte-Carlo (MCMC), Maximum Likelihood Estimation (MLE), Latin-Hypercube Sampling (LHS), Simulated Annealing (SA), Shuffled Complex Evolution Algorithm (SCE-UA), Differential Evolution Adaptive Metropolis Algorithm (DE-MCz), RObust Parameter Estimation (ROPE), Artificial Bee Colony (ABC), Dynamicallly Dimensioned Search algorithm (DDS), Pareto Archived Dynamicallly Dimensioned Search algorithm (PA-DDS) Fitness Scaled Chaotic Artificial Bee Colony (FSCABC) and Fourier Amplitude Sensitivity Test (FAST).

• Wide range of objective functions, likelihood functions and hydroligcal signatures to validate the sampled results. Available objective functions are: Bias, Nash-Sutcliff (NSE), log Nash-Sutcliff (logNSE), Logarithmic probability (logp), Correlation Coefficient (r), Coefficient of Determination (r^2), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Relative Root Mean Squared Error (RRMSE), Agreement Index (AI), Covariance, Decomposed MSE (dMSE) and Kling-Gupta Efficiency (KGE).

• Prebuild parameter distribution functions: Uniform, Normal, logNormal, Chisquare, Exponential, Gamma, Wald, Weilbull

• Suited to perform uncertainty-, sensitivity analysis or calibration of a model.

• Multi-objective support

• MPI support for fast parallel computing

• A progress bar monitoring the sampling loops. Enables you to plan your coffee breakes.

• Use of Numpy functions as often as possible. This makes your coffe breakes short.

• Different databases solutions: ram storage for fast sampling a simple and csv or sql tables the save solution for long duration samplings.

• Automatic best run selecting and plotting

• Parameter trace plotting

• Parameter interaction plot including the Gaussian-kde function

• Regression analysis between simulation and evaluation data

• Posterior distribution plot

• Convergence diagnostics with Gelman-Rubin and the Geweke plot

Relationship to other packages

A surprisingly small range of similar parameter estimation packages is available

• Pest Independent program for Model-Independent Parameter Estimation and Uncertainty Analysis
• OpenBugs Independent program for performing Bayesian inference Using Gibbs Sampling
• JAGS Independent program similar to OpenBUGS
• PyMC Comprehensive Python package to analyse models with MCMC techniques
• STAN Available in Python (amongst others) implementing MCMC techniques like NUTS, HMC and L-BFGS
• emcee Python package using a Affine Invariant Markov chain Monte Carlo Ensemble sampler
• BIP Python package for bayesian inference with a DREAM sampler

All of them have their pros and cons. To benchmark SPOTPY against these packages would be difficult because of wide variety of settings in different algorithms. The most related one is certainly PyMC, which brings many ideas into this framework. At the moment is PyMC limited to MCMC algorithms when analysing external deterministic models. To test other algorithms in such a straightforward way was the main reason why SPOTPY was developed. Consequently, none of the packages can offer such a wide range of different algorithms like SPOTPY.

Installation

Dependencies

The SPOTPY is an open-source package written in pure Python. It runs on all major platforms (Windows, Linux, Mac). SPOTPY requires just some standard packages:

• NumPy
• Scipy

Optional packages are:

• Matplotlib
• Pandas
• mpi4py

all packages are pre-installed e.g. in the following packages:

• Python xy version >3.5
• WinPython version >3.5
• Anaconda version >3.5

Download

SPOTPY is available on PYPI and GitHub. This should make installation easy, as you just have to use a command window and type

pip install spotpy

The recommended place for the SPOTPY package is in the site-packages folder in your Python Path, just the location of all other Python packages.

Project layout

SPOTPY can work with any parameter distributions. A standard setup uses pre-build distributions from NumPy. To benchmark the model-runs with a value, SPOTPY comes along with a wide range of pre-build objective functions. All algorithms realized in the SPOTPY package can work with the Distributions and objective functions. One can use them for uncertainty-, sensitivity analysis or parameter optimization. The three packages together can be run in any combination and results are stored in the ram storage or in a csv file. The results can be analysed with some pre-build statistics and plotting features.

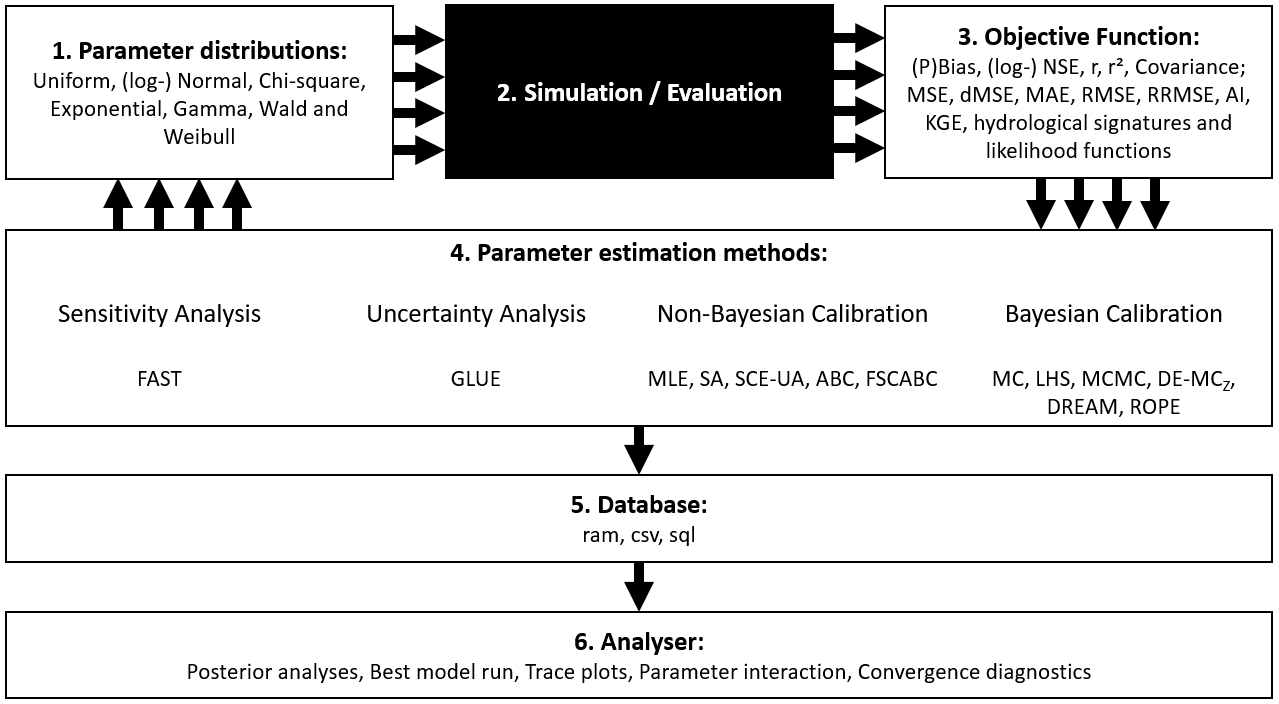
Above: Overview about functionality of the SPOTPY package

__init__.py             # Ensures that all needed files are loaded.
analyser.py             # Plotting features and statistic analysis.
database.py             # Ensures a secure data harbour during the sampling.
objectivefunctions.py   # Library of pre-build evaluation functions
likelihoods.py          # Library of pre-build evaluation functions
signatures.py           # Library of pre-build evaluation functions

algorithms/
    __init__.py   # Ensures the availability of all algorithms
    demcz.py      # Differential Evolution Markov Chain Monte Carlo
    lhs.py        # Latin Hypercube Sampling
    mcmc.py       # Metropolis Markov Chain Monte Carlo
    mle.py        # Maximum Likelihood Estimation
    mc.py         # Monte Carlo
    sceua.py      # Shuffled Complex Evolution
    sa.py         # Simulated annealing
    rope.py       # RObust Parameter Estimation
    fast.py       # Fourier Amplitude Sensitivity Testing
    abc.py        # Artificial Bee Colony
    fscabc.py     # Fitness Scaled Chaotic Artificial Bee Colony
    dream.py      # Differential Evolution Adaptive Metropolis
    dds.py        # Dynamically Dimensioned Search


parallel/
    mpi.py        #Basic Parralel Computing features 
    mpipool.py    #Basic Parralel Computing features 
    mproc.py      #Basic Parralel Computing features 
    sequential.py #Basic Parralel Computing features

examples/
    spotpy_setup_ackley.py      # Example SPOTPY setup to analyse the Ackley function 
    spotpy_setup_griewank.py    # Example SPOTPY setup to analyse the Griewank function
    spotpy_setup_rosenbrock.py  # Example SPOTPY setup to analyse the Rosenbrock function
    getting_started.py          # Recommended test file for starters

tutorials/
    tutorial_rosenbrock.py      # Source code for the Rosenbrock example the Tutorial
    tutorial_griewank.py        # Source code for the Rosenbrock example the Tutorial
    tutorial_ackley.py          # Source code for the Rosenbrock example the Tutorial
    tutorial_Parameterlist_iterator.py        # Example how to sample given parameter combinations